|

En el mundo de la electrónica existe una gran variedad de formas de onda necesarias para alcanzar diversos fines, ya que, cada tipo de onda tiene sus propias características.
En esta lección haremos un breve recorrido por los tipos de onda periódicas más habituales que nos podemos encontrar en multitud de circuitos de diferentes campos: electrónica de comunicaciones, electrónica industrial, informática, audio analógico/digital...
Puedes ver online una simulación de este tipo de señales: simulación online.

Una onda periódica es una señal eléctrica alterna que se repite indefinidamente, y sin alteración, a lo largo del tiempo.
Por lo tanto, vamos a encontrarnos que todos y cada uno de los ciclos de cualquiera de estas ondas va a necesitar de un tiempo para ir "dibujándose" (formándose) al 100%.
Este tiempo se llama: periodo (T). Dependiendo de su valor, y por su repetitividad, le corresponde una determinada frecuencia (f).
El PERIODO (T) es el tiempo que tarda en "dibujarse" un ciclo al completo y su resultado se da en segundos (o en submúltiplos del segundo).
La FRECUENCIA (f) es el número de ciclos que se "dibujan" en 1 segundo y su resultado se da en ciclos por segundo (c.p.s.) o en Hertzios (Hz), que viene a ser lo mismo.
Conocido el periodo o la frecuencia de una señal, podemos calcular el otro utilizando las sencillas fórmulas que aparecen en la figura de abajo: el periodo es la inversa de la frecuencia (T=1/f) y la frecuencia el inverso del periodo (f=1/T)
La onda senoidal (o sinusoidal) es una onda muy familiar ya que está presente en todo el sistema eléctrico de las viviendas (es uno más de la familia ;-).
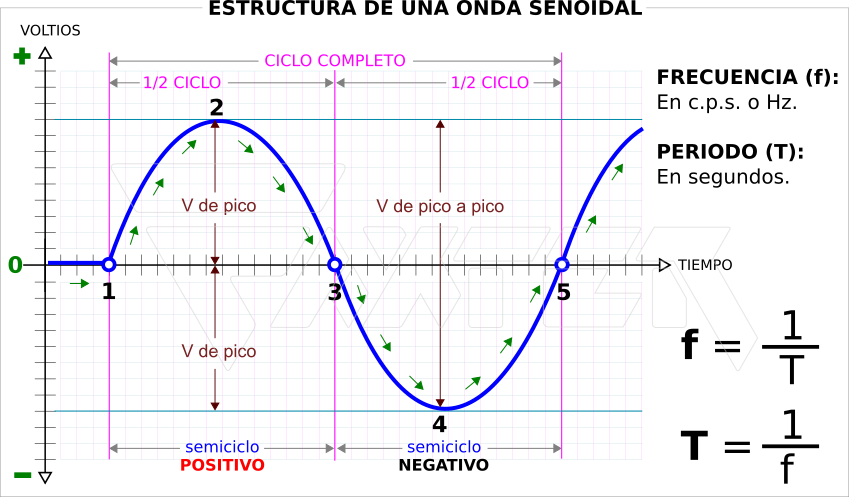
Como podemos ver en la gráfica superior, la señal empieza a dibujarse a partir del punto 1 y su valor en tensión es de 0 voltios en ese instante.
Continúa formándose alcanzando valores de tensión positivos cada vez más grandes hasta llegar al punto 2. En ese instante, si la tensión es de +10 voltios (p.ej.), diremos que la señal ha alcanzado su máximo valor positivo y ese valor, +10v, será su valor de pico positivo.
A partir de ese instante, el valor de la señal va decreciendo en tensión hasta llegar al punto 3 que será, de nuevo, 0v.
Desde el punto 1 al 3 se ha formado la mitad de la señal. Ese trozo se llama semiciclo positivo porque es la mitad de su ciclo completo y los valores que ha tomado durante todo ese tiempo fueron valores de tensión positivos (entre 0v y +10v).
Del punto 3 al 4 la señal continúa formándose pero, esta vez, tomando valores de tensión negativos, por debajo de 0v.
Cuando llega al punto 4 alcanza su máximo valor negativo y ese valor, -10v, será su valor de pico negativo.
El valor de pico positivo es igual al valor de pico negativo y la suma de ambos nos da el llamado valor de pico a pico.
En el caso de este ejemplo, el valor de pico a pico será de: 10+10 = 20v (no se tienen en cuenta los signos).
Del punto 4 al 5 la señal completa el 100% del ciclo, tomando esta vez valores menos negativos hasta llegar a los 0v. A partir de ahí comienza a repetirse.
Desde el punto 3 al 5 se ha formado la otra mitad de la señal. Ese trozo se llama semiciclo negativo porque es la otra mitad de su ciclo completo y los valores que ha tomado durante todo ese tiempo fueron valores de tensión negativos (ente 0v y -10v).
La señal ha tardado su tiempo en llegar del punto 1 al 5. Como en ese tiempo se ha formado su ciclo al 100% (se ha "dibujado" la onda al completo), el tiempo invertido en ello será el periodo (T). A dicho periodo le corresponde una frecuencia (f) determinada.
# Ejemplo:
Si cada ciclo completo de la señal ha tardado en formarse 0,02 segundos, su frecuencia será de 50Hz (f=1/0,02) que es la frecuencia típica de la onda senoidal presente en la red eléctrica de muchos países.
A la inversa. Si conocemos la frecuencia de una onda, p.ej. 60Hz, podemos saber el tiempo que ha invertido en formar cada uno de sus ciclos, o sea, su periodo: 0,017 segundos (T=1/60).
La onda senoidal se considera una onda pura. Carece de armónicos, es simétrica (sus dos semiciclos son idénticos) y no tiene cambios bruscos en su forma.
Además de estar presente en la red eléctrica es utilizada para muchos otros fines. Podemos ver que, generalmente junto a otro tipo de ondas, la onda senoidal forma parte de equipos generadores de ondas para realizar pruebas y ajustes.
Con la combinación de varias ondas senoidales podemos conseguir fabricar cualquier tipo de onda (según transformada de Fournier).
La onda cuadrada es también una onda muy popular y está asociada con las ondas de tipo digital por tener un carácter binario.
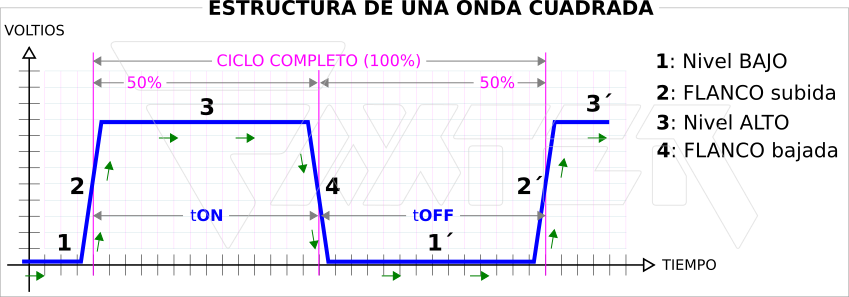
Según se puede apreciar en la gráfica superior, la onda cuadrada está formada por dos niveles de tensión: uno alto y otro bajo.
Partiendo de un nivel de 0 voltios (punto 1), la señal da un salto brusco a un nivel alto de tensión (p.ej. +5v, +9v, +12v...) pero ese salto no es instantáneo, por eso se puede apreciar una pequeña inclinación en su paso de 0v a +Xv (tramo 2). Este tramo se llama flanco de subida o flanco ascendente porque los niveles de tensión que va tomando la onda van subiendo (aumentando de valor).
Una vez que la señal alcanza su máximo valor (tramo 3), se mantiene sin variación durante un tiempo que llamamos: tON, o sea el tiempo en el que la señal toma un valor fijo:+Xv.
Terminado ese tiempo, la señal da otro salto brusco hacia 0v (tramo 4). Igual que sucedía con el tramo 2, al no ser instantáneo ese cambio aparece ahora un flanco de bajada o flanco descendente porque los niveles de tensión que va tomando la onda van bajando (disminuyendo de valor).
Despreciando el tiempo consumido en los flancos (que es insignificante), la señal ocupa el 50% del tiempo del ciclo en mantenerse a nivel alto (tON).
Una vez concluido el flanco de bajada, la señal se mantiene a ese nivel bajo (tramo 1´) de 0v el resto del tiempo del ciclo (el otro 50%) y a ese tiempo le llamamos: tOFF. A partir de ese instante la señal comienza a repetirse.
La suma de los tiempos tON + tOFF, como corresponde al 100% del ciclo de la onda, nos da el periodo (T) de la señal.
Aunque no vamos a tratar este tema, apuntar que destacamos el asunto de los flancos porque hay circuitos que son capaces de detectar eses flancos y operar en función de si han detectado un flanco de uno u otro tipo.
Como vemos, la onda cuadrada se compone de dos niveles de tensión, uno significativamente más alto (más positivo) que el otro.
En lógica positiva, el valor más alto se le suele nombrar como estado en ON (encendido) o con el valor numérico: 1 y el valor más bajo como estado en OFF (apagado) o con el valor numérico 0.
Así, una secuencia de estados de la onda cuadrada podríamos representarlo así: ON-OFF-ON-OFF... o así: 1-0-1-0...
La onda cuadrada es rica en armónicos impares y se utiliza en multitud de circuitos, sobre todo en aquellos que hacen la función de marcadores de tiempo (también llamados: relojes) para sincronizar operaciones que deben realizar otros circuitos.
También son muy utilizadas en analizadores de circuitos digitales, temporizadores, etc.
Una variante de la onda cuadrada es la ONDA RECTANGULAR.
Esta onda se diferencia de la cuadrada en que los tiempos tON y tOFF son diferentes del 50%. P.ej.: 70% y 30%, 25% y 75% ...
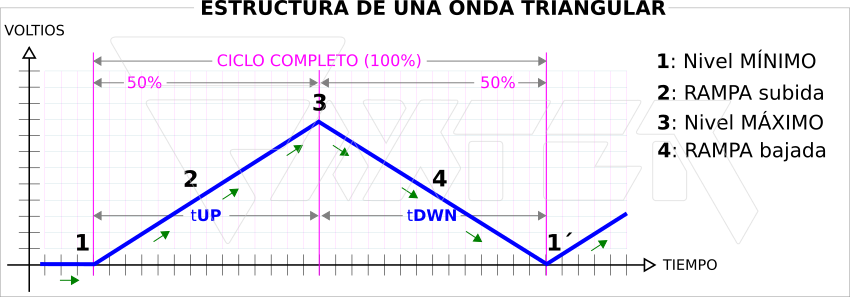
La onda triangular se empieza a formar a partir de un valor de tensión bajo o nivel mínimo (punto 1), en este caso de 0v.
Comienza a aumentar su valor de forma lineal (tramo 2) hasta alcanzar su valor de tensión máximo o nivel máximo (punto 3) formando una rampa de subida (porque sus niveles de tensión han ido subiendo cada instante).
El tiempo transcurrido en formarse esa rampa es el 50% de su ciclo completo y le llamamos: tiempo de subida o tUP.
Alcanzado el nivel máximo (punto 3), la señal comienza ahora a disminuir su valor de forma lineal (tramo 4) hasta llegar, de nuevo, al valor mínimo (punto 1´) formando una rampa de bajada (porque sus niveles de tensión han ido bajando cada instante). A partir de este punto, la señal comienza a repetirse.
El tiempo transcurrido en formarse esa rampa es el otro 50% de su ciclo completo y le llamamos: tiempo de bajada o tDWN.
La suma de los tiempos tUP + tDWN, como corresponde al 100% del ciclo de la onda, nos da el periodo (T) de la señal.
La onda triangular, como la onda cuadrada, es rica en armónicos impares y se utiliza habitualmente en circuitos que necesitan realizar barridos, como es el caso de osciloscopios y televisores.
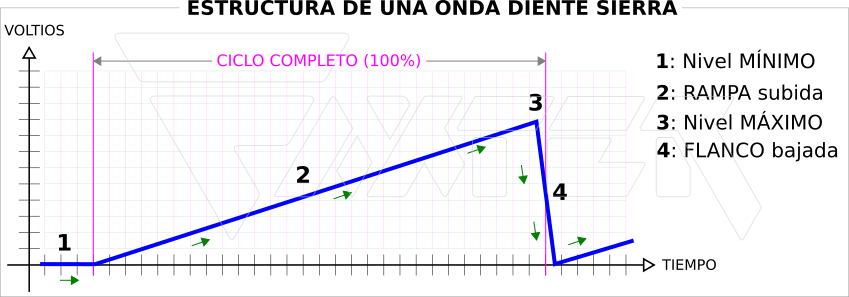
La onda en diente de sierra, partiendo de un nivel bajo o nivel mínimo (punto 1), va aumentando su valor de forma lineal (tramo 2) hasta alcanzar su valor de tensión máximo o nivel máximo (punto 3), formando una rampa de subida.
Desde el punto 3 sufre un brusco descenso hacia 0v (en este caso) terminando ahí su ciclo con un flanco de bajada. A partir de ese instante, la señal comienza a repetirse.
La onda ha empleado el 100% del tiempo de su ciclo en formar esa rampa ascendente. Por lo tanto, ese tiempo es su periodo (T).
Una onda como esta, invertida horizontalmente, también sería una onda de tipo diente de sierra. En este caso, empezaría con el nivel más alto de voltaje (con un flanco de subida), continuaría con una larga rampa descendente y terminaría en su nivel más bajo.
Las ondas en diente de sierra son muy ricas en armónicos (pares e impares). Como el caso de las ondas triangulares también son muy utilizadas en aquellos circuitos que necesitan hacer barridos.
Gracias a su riqueza de armónicos es una onda muy apreciada para conseguir sonidos y efectos de sonido sintetizados. En nuestro BLOG, en el artículo llamado: TRAUTONIUM, el padre de los sintetizadores , capítulo "El invento", se habla de este tema.

La onda en escalera empieza en su nivel de tensión más bajo o nivel mínimo (0v en este caso) y gradualmente, a saltos, va aumentando su nivel de tensión (niveles intermedios) hasta alcanzar su nivel más alto o nivel máximo (tramo 6).
Seguidamente, cae bruscamente al nivel mínimo formando un flanco de bajada. A partir de ese instante, la señal comienza a repetirse.
La onda ha empleado el 100% del tiempo de su ciclo en formar esa escalera ascendente. Entonces, ese tiempo será su periodo (T).
Esta onda, invertida horizontalmente (es decir, con una escalera descendente), también sería una onda de tipo en escalera.
Una de las aplicaciones más populares de este tipo de onda es su utilidad para realizar operaciones de muestreo de señales, sobre todo en los conversores A/D (analógico/digitales).
Estos tipos de onda que hemos visto están presentes en multitud de circuitos electrónicos, sobre todo en los de tipo digital. Sería prácticamente imposible que dichos circuitos pudieran ejercer sus funciones sin su participación.
En las ondas ideales no existen los flancos (ni de subida, ni de bajada), pero nosotros los hemos "pintado" porque existen en la práctica y tienen su relevancia.
Los flancos, realmente son rampas muy, muy, cortas y empinadas que se producen a gran velocidad. Lo ideal sería que no se produjeran pero, como no es posible eliminarlos, hay que convivir con ellos.
Son el resultado de la conmutación interna de los circuitos generadores de ondas, que son incapaces de hacer cambios significativos de tensión (de 1 a 0, o de 0 a 1) de forma instantánea.
Por el contrario, las rampas, son progresiones más largas que se producen con más lentitud y son buscadas a propósito para que realicen determinadas funciones.
Esa es, en esencia, la diferencia entre flancos y rampas.
|